5.1.3 Cartesian Power projection

Figure 5.5: Exponential or power transformation of $x$-coordinates.

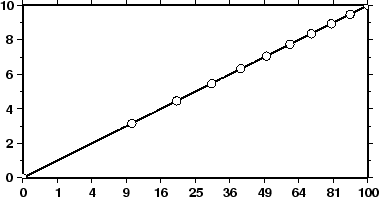
This projection uses $u' = a u^b + c$ and allows us to explore exponential relationships like x$^p$ versus y$^q$. While $p$ and $q$ can be any values, we will select $p = 0.5$ and $q = 1$ which means we will plot $x$ versus $\sqrt {x}$. We indicate this scaling by appending a p (lower case P) followed by the desired exponent, in our case 0.5. Since $q = 1$ we do not need to specify p1 since it is identical to the linear transformation. Thus our command becomes

psxy -R0/100/0/10 -Jx0.3ip0.5/0.15i -Ba1p/a2f1WSne -W1p -P -K sqrt.d > GMT_pow.ps
psxy -R -Jx -Sc0.075i -Gwhite -W -O sqrt.d10 >> GMT_pow.ps