



Next: Acknowledgments
Up: The Generic Mapping Tools
Previous: List of Tables
Contents
Index
- 4.1. Some GMT parameters that affect plot appearance.
- 4.2. More GMT parameters that affect plot appearance.
- 4.3. Even more GMT parameters that affect plot appearance.
- 4.4. The plot region can be specified in two different ways. (a) Extreme values
for each dimension, or (b) coordinates of lower left and upper right corners.
- 4.5. The 29 map projections and coordinate transformations available in GMT.
- . Geographic map border using separate selections for annotation,
frame, and grid intervals. Formatting of the annotation is controlled by
the parameter PLOT_DEGREE_FORMAT in your .gmtdefaults4 file.
- 4.7. Geographic map border with both primary (P) and secondary (S) components.
- 4.8. Linear Cartesian projection axis. Long tickmarks accompany
annotations, shorter ticks indicate frame interval. The axis label is
optional. We used -R0/12/0/1 -JX3/0.4
-Ba4f2g1:Frequency::,%:.
- 4.9. Logarithmic projection axis using separate values for annotation,
frame, and grid intervals. (top) Here, we have chosen to annotate the actual
values. Interval = 1 means every whole power of 10, 2 means 1, 2, 5 times
powers of 10, and 3 means every 0.1 times powers of 10. We used
-R1/1000/0/1 -JX3l/0.4 -Ba1f2g3.
(middle) Here, we have chosen to
annotate log
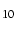 of the actual values, with -Ba1f2g3l.
(bottom) We annotate every power of 10 using log
of the actual values, with -Ba1f2g3l.
(bottom) We annotate every power of 10 using log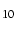 of the actual values
as exponents, with -Ba1f2g3p.
of the actual values
as exponents, with -Ba1f2g3p.
- 4.10. Exponential or power projection axis. (top) Using an exponent of 0.5
yields a
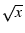 axis. Here, intervals refer to actual data values, in
-R0/100/0/1 -JX3p0.5/0.4 -Ba20f10g5.
(bottom) Here, intervals refer to projected values, although the annotation
uses the corresponding unprojected values, as in -Ba3f2g1p.
axis. Here, intervals refer to actual data values, in
-R0/100/0/1 -JX3p0.5/0.4 -Ba20f10g5.
(bottom) Here, intervals refer to projected values, although the annotation
uses the corresponding unprojected values, as in -Ba3f2g1p.
- 4.11. Cartesian time axis, example 1.
- 4.12. Cartesian time axis, example 2.
- 4.13. Cartesian time axis, example 3.
- 4.14. Cartesian time axis, example 4.
- 4.15. Cartesian time axis, example 5.
- 4.16. Cartesian time axis, example 6.
- 4.17. Cartesian time axis, example 7.
- 4.18. Users can specify Landscape [Default] or Portrait (-P) orientation.
- 4.19. A final PostScript file consists of a stack of individual pieces.
- 4.20. The -U option makes it easy to ``date'' a plot.
- 4.21. Plot origin can be translated freely with -X -Y.
- 5.1. Linear transformation of Cartesian coordinates.
- 5.2. Linear transformation of map coordinates.
- 5.3. Linear transformation of calendar coordinates.
- 5.4. Logarithmic transformation of
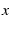 -coordinates.
-coordinates.
- 5.5. Exponential or power transformation of
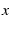 -coordinates.
-coordinates.
- 5.6. Polar (Cylindrical) transformation of
(
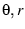 ) coordinates.
) coordinates.
- 6.1. Albers equal-area conic map projection
- 6.2. Lambert conformal conic map projection
- 6.3. Equidistant conic map projection
- 6.4. Rectangular map using the Lambert
azimuthal equal-area projection.
- 6.5. Hemisphere map using the Lambert
azimuthal equal-area projection.
- 6.6. Equal-Area (Schmidt) and Equal-Angle (Wulff) stereo nets.
- 6.7. Polar
stereographic conformal projection.
- 6.8. Polar
stereographic conformal projection with rectangular borders.
- 6.9. General
stereographic conformal projection with rectangular borders.
- 6.10. Hemisphere map using the Orthographic projection.
- 6.11. World map using the equidistant azimuthal projection.
- 6.12. Gnomonic azimuthal projection.
- 6.13. Simple Mercator map.
- 6.14. Rectangular Transverse Mercator map.
- 6.15. A global Transverse Mercator map.
- 6.16. Oblique Mercator map using -Joc. We
make it clear which direction is North by adding a star rose with the -T option.
- 6.17. Cassini map over Sardinia.
- 6.18. World map using the equidistant cylindrical projection.
- 6.19. World map using the Behrman cylindrical projection.
- 6.20. World map using the Miller cylindrical projection.
- 6.21. World map using the Hammer projection.
- 6.22. World map using the Mollweide projection.
- 6.23. World map using the Winkel Tripel projection.
- 6.24. World map using the Robinson projection.
- 6.25. World map using the Eckert IV projection.
- 6.26. World map using the Eckert VI projection.
- 6.27. World map using the Sinusoidal projection.
- 6.28. World map using the Interrupted Sinusoidal projection.
- 6.29. World map using the Van der Grinten projection.
- 7.1. Contour maps of gridded data.
- 7.2. Color images from gridded data.
- 7.3. Spectral estimation and
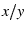 -plots.
-plots.
- 7.4. 3-D perspective mesh plot.
- 7.5. 3-D illuminated surface.
- 7.6. Two kinds of histograms.
- 7.7. A typical location map.
- 7.8. A 3-D histogram.
- 7.9. Time-series as ``wiggles'' along a track.
- 7.10. Geographical bar graph.
- 7.11. The RGB color cube.
- 7.12. Optimal triangulation of data.
- 7.13. Display of vector fields in GMT.
- 7.14. Gridding of data and trend surfaces.
- 7.15. Gridding, contouring, and masking of data.
- 7.16. More ways to grid data.
- 7.17. Clipping of images using coastlines.
- 7.18. Volumes and geo-spatial selections.
- 7.19. Using color patterns in illustrations.
- 7.20. Making a new volcano symbol for GMT.
- 7.21. Using custom symbols in GMT.
- 7.22. Time-series of RedHat stock price since IPO.
- 7.23. World-wide seismicity the last 7 days.
- 7.24. All great-circle paths lead to Rome.
- 7.25. Data selection based on geospatial criteria.
- 7.26. Global distribution of antipodes.
- B.1. Grid line registration of data nodes.
- B.2. Pixel registration of data nodes.
- F.1. Octal codes and corresponding symbols for StandardEncoding fonts.
- F.2. Octal codes and corresponding symbols for ISOLatin1Encoding fonts.
- F.3. Octal codes and corresponding symbols for the Symbol font.
- F.4. Octal codes and corresponding symbols for ZapfDingbats font.
- G.1. The standard 35 PostScript fonts recognized by GMT.
- J.1. Impulse responses for GMT filters.
- J.2. Transfer functions for 1-D GMT filters.
- J.3. Transfer functions for 2-D (radial) GMT filters.
- K.1. Map using the crude resolution coastline data.
- K.2. Map using the low resolution coastline data.
- K.3. Map using the intermediate resolution coastline data. We
have added a compass rose just because we have the power to do so.
- K.4. Map using the high resolution coastline data.
- K.5. Map using the full resolution coastline data.
- M.1. The standard 20 cpt files supported by GMT.
- N.1. Custom plot symbols supported by GMT.
- N.2. Additional custom plot symbols
- O.1. Equidistant contour label placement with -Gd, the only algorithm
available in previous GMT versions.
- O.2. Placing one label per contour that exceed 1 inch in length,
centered on the segment with -Gn.
- . Four labels are positioned on the points along the contours that
are closest to the locations given in the file fix.d in the -Gf option.
- O.4. Labels are placed at the intersections between contours and the
great circle specified in the -GL option.
- O.5. Labels are placed at the intersections between contours and the
multi-segment lines specified in the -GX option.
- O.6. Labels attributes are controlled with the arguments to the -Sq option.
- O.7. Another label attribute example.
- O.8. Labels based on another data set (here bathymetry) while
the placement is based on distances.
- O.9. Tsunami travel times from the Canary Islands to places
in the Atlantic, in particular New York. Should a catastrophic landslide occur
it is possible that New York will experience a large tsunami about 8 hours after
the event.




Next: Acknowledgments
Up: The Generic Mapping Tools
Previous: List of Tables
Contents
Index
Paul Wessel
2004-10-01